(Canadian Senior Mathematics Contest 2021, Part A, Question 6, CEMC - UWaterloo)

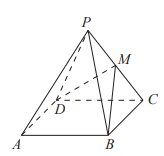
In the diagram, $PABCD$ is a pyramid with square base $ABCD$ and with $PA = PB = PC = PD$. Suppose that $M$ is the midpoint of $PC$ and that $\angle BMD = 90^{\circ}$. Triangular-based pyramid $MBCD$ is removed by cutting along the triangle defined by the points $M$, $B$ and $D$. The volume of the remaining solid $PABMD$ is $288$. What is the length of $AB$?


Answer Submission Note(s)
Your answer should be of the form "x * sqrt(y)".